第一类重要极限
$$
\lim\limits_{x\rightarrow{0}} \frac{\sin{x}}{x} = 1
$$
第二类重要极限
$$
\lim\limits_{x\rightarrow\infty}(1+\frac{1}{x})^{x} = \lim\limits_{x\rightarrow\infty}{e}^{x\cdot\ln{(1+\frac{1}{x})}}=\lim\limits_{x\rightarrow\infty}e^{{x}\cdot{\frac{1}{x}}}=e
$$
$\frac{0}{0}$ 型等价无穷小量
| 等价公式 |
广东普通专升本 |
重要程度 |
| $\sin x \sim x$ |
√ |
|
| $\arcsin x \sim x$ |
√ |
|
| $\tan x \sim x$ |
√ |
|
| $\arctan x \sim x$ |
√ |
|
| $e^x-1 \sim x$ |
√ |
$\bigstar$ |
| $ln(1+x) \sim x$ |
√ |
$\bigstar$ |
| $1-\cos x \sim \frac{1}{2}x^2$ |
√ |
$\bigstar$ |
| $\sqrt[n]{1+x}-1 \sim \frac{x}{n} \iff (1+ax)^b-1 \sim abx (特点是 -1)$ |
√ |
$\bigstar$ |
| $x-\sin x \sim \frac{1}{6}x^3$ |
|
|
| $\tan x-x \sim \frac{1}{3}x^3$ |
|
|
| $\tan x-\sin x \sim \frac{1}{2}x^3$ |
|
|
| $a^x-1 \sim x\ln a$ |
|
|
| $\ln(1+x)-x \sim -\frac{1}{2}x^2$ |
|
|
导数公式
| 导数公式 |
广东普通专升本 |
重要程度 |
| $C^{'} = 0\ (C为常数)$ |
√ |
$\bigstar$ |
| $(x^a) = ax^{a-1}$ |
√ |
$\bigstar$ |
| $(\frac{1}{x})^{'} = -\frac{1}{x^2}$ |
√ |
$\bigstar$ |
| $(\sqrt{x})^{'} = \frac{1}{2\sqrt{x}}$ |
√ |
$\bigstar$ |
| $(a^x)^{'} = a^x\ln a\ (a > 0 且 a \ne 1)$ |
√ |
$\bigstar$ |
| $(e^x)^{'} = e^x$ |
√ |
$\bigstar$ |
| $(log_ax)^{'} = \frac{1}{xlna}\ (a > 0 且 a \ne 1)$ |
√ |
$\bigstar$ |
| $(lnx)^{'} = \frac{1}{x}$ |
√ |
$\bigstar$ |
| $(\sin x)^{'} = \cos x$ |
√ |
$\bigstar$ |
| $(\cos x)^{'} = -\sin x$ |
√ |
$\bigstar$ |
| $(\tan x)^{'} = \sec^2{x}$ |
√ |
$\bigstar$ |
| $(\cot x)^{'} = -\csc^2{x}$ |
√ |
$\bigstar$ |
| $(\sec x)^{'} = \sec x \cdot \tan x$ |
√ |
$\bigstar$ |
| $(\csc x)^{'} = -\csc x \cdot \cot x$ |
√ |
$\bigstar$ |
| $(\arcsin x)^{'} = \frac{1}{\sqrt{1-x^2}}$ |
√ |
$\bigstar$ |
| $(\arccos x)^{'} = -\frac{1}{\sqrt{1-x^2}}$ |
√ |
$\bigstar$ |
| $(\arctan x)^{'} = \frac{1}{1+x^2}$ |
√ |
$\bigstar$ |
| $(arccot\ {x})^{'} = -\frac{1}{1+x^2}$ |
√ |
$\bigstar$ |
不定积分
| 积分公式 |
广东普通专升本 |
重要程度 |
| $\int k \text{d}x = kx+C\ (k为常数)$ |
√ |
$\bigstar$ |
| $\int x^a \text{d}x = \frac{1}{a+1}x^{a+1} + C$ |
√ |
$\bigstar$ |
| $\int \frac{1}{\sqrt{x}} \text{d}x = 2\sqrt{x}+C$ |
√ |
$\bigstar$ |
| $\int \frac{1}{x^2} \text{d}x = -\frac{1}{x}+C$ |
√ |
$\bigstar$ |
| $\int \frac{1}{x} \text{d}x = \ln |x|+C$ |
√ |
$\bigstar$ |
| $\int e^x \text{d}x = e^x + C$ |
√ |
$\bigstar$ |
| $\int a^x \text{d}x = \frac{a^x}{\ln a}+C$ |
√ |
$\bigstar$ |
| $\int \cos{x}\text{d}x=\sin{x}+C$ |
√ |
$\bigstar$ |
| $\int \sin{x}\frac{x-1}{x+a}=-\cos{x}+C$ |
√ |
$\bigstar$ |
| $\int \tan{x}\text{d}x=-\ln{|\cos{x}|}+C$ |
√ |
$\bigstar$ |
| $\int \cot{x}\text{d}x=\ln|\sin{x}|+C$ |
√ |
$\bigstar$ |
| $\int \sec{x}\text{d}x=\ln|\sec{x}+\tan{x}|+C$ |
√ |
$\bigstar$ |
| $\int \csc{x}\text{d}x=\ln|\csc{x}-\cot{x}|+C$ |
√ |
$\bigstar$ |
| $\int \sec^2{x}\text{d}x=\tan{x}+C$ |
√ |
$\bigstar$ |
| $\int \csc^2{x}\text{d}x=-\cot{x}+C$ |
√ |
$\bigstar$ |
| $\int \sec{x}\tan{x}=\sec{x}+C$ |
√ |
$\bigstar$ |
| $\int \csc{x}\cot{x}\text{d}x=-\csc{x}+C$ |
√ |
$\bigstar$ |
| $\int \frac{1}{\sqrt{1-x^2}}\text{d}x=\arcsin{x}+C$ |
√ |
$\bigstar$ |
| $-\int\frac{1}{\sqrt{1-x^2}}\text{d}x=\arccos{x}+C$ |
√ |
$\bigstar$ |
| $\int\frac{1}{1+x^2}\text{d}x=\arctan{x}+C$ |
√ |
$\bigstar$ |
| $-\int\frac{1}{1+x^2}\text{d}x=arccot\ {x}+C$ |
√ |
$\bigstar$ |
| $\int \frac{1}{x^2-a^2} \text{d}x = \frac{1}{2a}\ln|\frac{x-1}{x+a}|+C$ |
|
|
| $\int\ln{x}\text{d}{x}=x\ln{x}-x+C$ |
|
|
| $\int{x}e^x\text{d}{x}=xe^x-e^x+C$ |
|
|
直角三角形
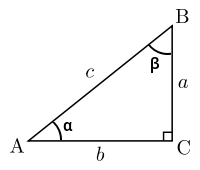
特殊三角函数值表
| 角度 |
$0^{\circ}$ |
$30^{\circ}$ |
$45^{\circ}$ |
$60^{\circ}$ |
$90^{\circ}$ |
$120^{\circ}$ |
$135^{\circ}$ |
$150^{\circ}$ |
$180^{\circ}$ |
| $\alpha的弧度$ |
$0$ |
$\frac{\pi}{6}$ |
$\frac{\pi}{4}$ |
$\frac{\pi}{3}$ |
$\frac{\pi}{2}$ |
$\frac{2\pi}{3}$ |
$\frac{3\pi}{4}$ |
$\frac{5\pi}{6}$ |
$\pi$ |
| $\sin\alpha$ |
$0$ |
$\frac{1}{2}$ |
$\frac{\sqrt{2}}{2}$ |
$\frac{\sqrt{3}}{2}$ |
$1$ |
$\frac{\sqrt{3}}{2}$ |
$\frac{\sqrt{3}}{2}$ |
$\frac{1}{2}$ |
$0$ |
| $\cos\alpha$ |
$1$ |
$\frac{\sqrt{3}}{2}$ |
$\frac{\sqrt{2}}{2}$ |
$\frac{1}{2}$ |
$0$ |
$-\frac{1}{2}$ |
$-\frac{\sqrt{3}}{2}$ |
$-\frac{\sqrt{3}}{2}$ |
$-1$ |
| $\tan\alpha$ |
$0$ |
$\frac{\sqrt{3}}{3}$ |
1 |
$\sqrt{3}$ |
不存在 |
$-\sqrt{3}$ |
$-1$ |
$-\frac{\sqrt{3}}{3}$ |
0 |
| $\cot\alpha$ |
$\infty$ |
$\sqrt{3}$ |
1 |
$\frac{\sqrt{3}}{3}$ |
0 |
$-\frac{\sqrt{3}}{3}$ |
$-1$ |
$-\sqrt{3}$ |
$\infty$ |
勾股定理
$$
a^2+ b^2 = c^2
$$
三角关系
|
三角关系公式 |
广东普通专升本 |
重要程度 |
| 正弦 |
$\sin \alpha = \frac{a}{c} = \frac{对边}{斜边}$ |
|
|
| 余弦 |
$\cos \alpha = \frac{b}{c} = \frac{邻边}{斜边}$ |
|
|
| 正切 |
$\tan \alpha = \frac{a}{b} = \frac{对边}{邻边}$ |
|
|
| 余切 |
$\cot \alpha = \frac{b}{a} = \frac{邻边}{对边}$ |
|
|
| 正割 |
$\sec\alpha=\frac{c}{b}=\frac{斜边}{邻边}$ |
|
|
| 余割 |
$\csc\alpha=\frac{c}{a}=\frac{斜边}{对边}$ |
|
|
三角函数转换
- $\sec \alpha = \frac{1}{\cos \alpha}$
- $\csc \alpha = \frac{1}{\sin \alpha}$
- $\frac{1}{\cos^2{x}}=\sec^2{x}$
常见三角函数化简公式
- 平方和
- $\sin^{2}x + \cos^{2}x = 1$
- $1+\tan^{2}x = \sec^{2}x$
- $1+\cot^{2}x = csc^{2}x$
- 二倍角
- $\sin{2x} = 2\sin{x}cos{x}$
- $\cos{2x} = \cos^{2}x - \sin^{2}x = 1 - 2\sin^{2}x = 2\cos^{2}x - 1$
- 降次
- $\sin^{2}x = \frac{1-\cos{2x}}{2}$
- $\cos^{2}x = \frac{1+\cos{2x}}{2}$
