第一章 函数与极限
函数的四大性质
奇偶性
偶函数
$$ f(-x) = f(x) $$
$$ f(x) + f(-x) => 偶函数 $$
奇函数
$$ f(-x) = -f(x) $$
$$ f(x) - f(-x) => 奇函数 $$
常见的奇函数和偶函数
- 奇函数
$$ x^{奇数}、sinx、arcsinx、tanx、arctanx $$
- 偶函数
$$ x^{偶数}、cosx、|x|、常数c $$
奇偶函数四则运算性质
- $奇 \pm 奇 = 奇$
- $偶 \pm 偶 = 偶$
- $奇 \pm 偶 = 非奇非偶$
- $奇 \times / \div 奇 = 偶$
- $奇 \times / \div 偶 = 奇$
- $偶 \times / \div 偶 = 偶$
复合函数的奇偶性
- $奇(奇) = 奇$
- $奇(偶) = 偶$
- $偶(奇) = 偶$
全奇则奇，遇偶则偶
有界性
单调性
有一函数 $f(x)$
- 当 $x_1 \lt x_2$ 时， $f(x_1) \lt f(x_2)$ 则 $f(x)$ 是单调递增函数
- 当 $x_1 \lt x_2$ 时， $f(x_1) \gt f(x_2)$ 则 $f(x)$ 是单调递减函数
周期性
极限
函数极限
$$ \lim\limits_{x\rightarrow{x_0}}f(x) = A $$
A 为确定的数
四则运算
设 $\lim\limits_{}f(x) = A$ 和 $\lim\limits_{}g(x) = B$ $$ \lim\limits_{}[f(x) \pm g(x)] = \lim\limits_{}f(x) \pm \lim\limits_{}g(x) = A \pm B $$
$$ \lim\limits_{}[f(x) \cdot g(x)] = \lim\limits_{}f(x) \cdot \lim\limits_{}g(x) = A \cdot B $$
$$ \lim\limits_{}\frac{f(x)}{g(x)} = \frac{\lim\limits_{}f(x)}{\lim\limits_{}g(x)} = \frac{A}{B} (B \ne 0) $$
前提条件：极限存在
两个重要的极限
第一类重要极限
$$ \lim\limits_{x\rightarrow{0}} \frac{\sin{x}}{x} = 1 $$
第二类重要极限
$$ \lim\limits_{x\rightarrow\infty}(1+\frac{1}{x})^{x} = \lim\limits_{x\rightarrow\infty}{e}^x\ln{(1+\frac{1}{x})}=\lim\limits_{x\rightarrow\infty}e^{{x}\cdot{\frac{1}{x}}}=e $$
数列极限
$$ \lim\limits_{x\rightarrow\infty}x_n = B $$
B 为确定的数
$x_n\rightarrow\infty$ => $x_n\rightarrow{A}$ 则 $x_{2n+1}\rightarrow {A}$ 、 $x_{2n}\rightarrow {A}$
左右极限
- 左极限
$$ \lim\limits_{x\rightarrow x_0^-}f(x) $$
- 右极限
$$ \lim\limits_{x\rightarrow x_0^+}f(x) $$
极限存在
左右极限存在且相等
$f(x)$ 在某点 $x_0$ 处的极限值，与 $f(x)$ 在该店无定义/ $f(x_0)$ 无关
极限七兄弟
$\frac{\infty}{\infty}$ 型
-
定义：分子 $\rightarrow\infty$ ， 分母 $\rightarrow\infty$ 的极限
-
解法：抓大头
-
题型
- 幂函数：指数越大值越大
- 指数函数：底数越大值越大
- 通过抓大头求参数
- 分母最高次 = 分子最高次 值为非零常数
- 分母最高次 > 分子最高次 值为0
$\frac{0}{0}$ 型
-
定义：分子 $\rightarrow 0 $ ， 分母 $\rightarrow 0 $ 的极限
-
解法：利用等价无穷小量求解
-
常见等价公式
$$ \left { \begin{array}{c} sinx \sim x \ arcsinx \sim x \ \end{array} \right. \ \left { \begin{array}{c} tanx \sim x \ arctanx \sim x \ \end{array} \right. \ \left { \begin{array}{c} e^x-1 \sim x \ ln(1+x) \sim x \ \end{array} \right. $$
$$ 1-cosx \sim \frac{1}{2}x^2 $$
$$ \sqrt[n]{1+x}-1 \sim \frac{x}{n} \iff (1+ax)^b-1 \sim abx (特点是 -1) $$
$$ \left { \begin{array}{c} x-sinx \sim \frac{1}{6}x^3 \ tanx-x \sim \frac{1}{3}x^3 \ tanx-sinx \sim \frac{1}{2}x^3 \ \end{array} \right. $$
$$ \left { \begin{array}{c} a^x-1 \sim xlna \ ln(1+x)-x \sim -\frac{1}{2}x^2\ \end{array} \right. $$
$0 \cdot \infty$ 型
$$ 0 \cdot \infty \Rightarrow \left { \begin{array}{c} 对0取倒数，下放分母： 0 \cdot \infty = \frac{\infty}{\frac{1}{0}} = \frac{\infty}{\infty} & \ 对 \infty 取倒数，下放分母： 0 \cdot \infty = \frac{\infty}{\frac{1}{\infty}} = \frac{0}{0} & \ \end{array} \right. $$
下放原则
- 一般来讲，下放简单易求导的函数
- 遇到有三角函数( $tanx, cotx$ ), 先化简
$$ \left { \begin{array}{c} tanx = \frac{sinx}{cosx} \ cotx = \frac{cosx}{sinx} \ secx = \frac{1}{cosx} \ \end{array} \right. $$
$$ 幂 \cdot 对数 \Rightarrow x^a \cdot ln x = 0 $$
$\infty - \infty$ 型
- 分式 =》 通分
- 根式 =》有理化（利用 $(a+b)(a-b)=a^2-b^2$ 去根号）
$u^v$ 型
-
$1^\infty$
-
第二极限：$\lim\limits_{x\rightarrow 0}(1+x)^{\frac{1}{x}} = e$
-
解法
-
$$ u^v \Rightarrow e^{\lim\limits_{}(u-1) \cdot v} $$
-
$$ 次方很多 \Rightarrow e^{lnx} = x \Leftrightarrow u^v = e^{v \cdot lnu}(幂指函数对数化) $$
-
-
-
不是 $1^\infty (0^0,\infty^0)$
- $$ u^v = e^{v \cdot \ln{u}}(复合型极限) $$
易错考点=> $0 \cdot 有界 = 0$
遇到 $sin\infty,cos\infty,arctan\infty$ ，优先考虑 $0 \cdot 有界 = 0$
洛必达法则
$\lim\frac{f(x)}{g(x)}$ 是 $\frac{0}{0},\frac{\infty}{\infty}$
$$ \lim\frac{f(x)}{g(x)} => \lim\frac{f(x)^{'}}{g(x)^{'}} => \lim\frac{f(x)^{''}}{g(x)^{''}}= … = A $$
- 分子分母各自同事求导
- 洛必达法则，一般会配合等价使用(万事不对洛必达！)
夹逼定理
定义
若函数 $f(x)、g(x)、h(x)$ ，在 $x_0$ 的领域范围内有 $$ f(x) \leq g(x) \leq h(x) $$ 当 $\lim\limits_{x\rightarrow x_0}f(x)=\lim\limits_{x\rightarrow x_0}g(x)=A$ 时，则 $\lim\limits_{x\rightarrow x_0}g(x)=A$
使用条件
使用步骤
- 确认极限项数 $n$
- 确定最小项，确定最大项
- 去极限
$$ n \cdot 最小项极限 \leq 待求极限 \leq n \cdot 最大项极限 $$
- 由夹逼定理出结果
函数的左右极限
左极限：$\lim\limits_{x\rightarrow x_0^-}f(x)$ ，右极限：$\lim\limits_{x\rightarrow x_0^+}f(x)$ ，极限存在 $\Longleftrightarrow$ 左右极限存在且相等
与左右极限相关的函数
- 分段函数：以分段点为界，左边一个函数，右边一个函数
遇到分段函数 => 考虑左右极限
- $y=\frac{1}{x}$
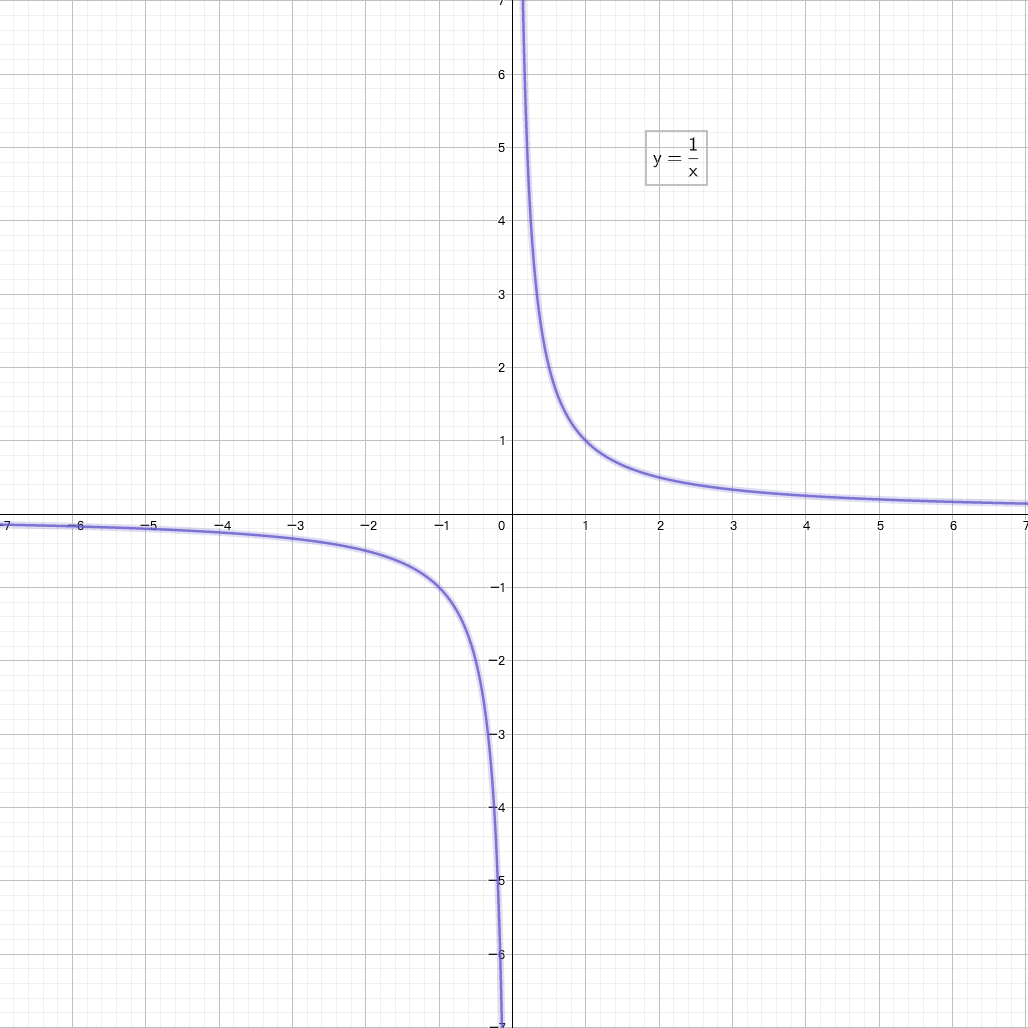$$
x \rightarrow 0 \
x \rightarrow 0^+ \Longrightarrow \frac{1}{x} \rightarrow +\infty \
x \rightarrow 0^- \Longrightarrow \frac{1}{x} \rightarrow -\infty
$$
- 指数函数 $y=e^x$
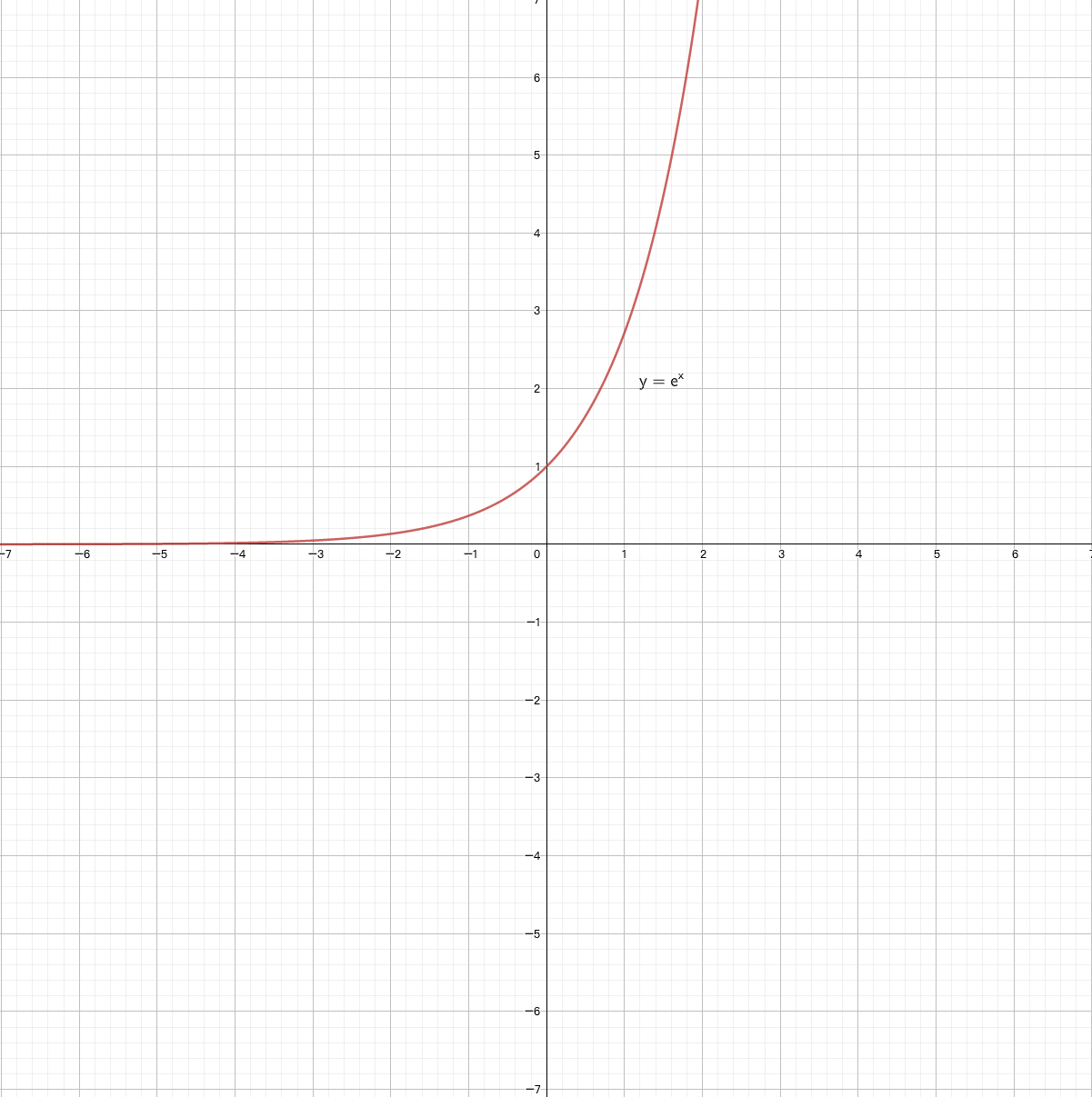$$
x \rightarrow \infty \
x \rightarrow +\infty \Longrightarrow e^x \rightarrow +\infty \Longrightarrow e^{+\infty} \rightarrow +\infty\
x \rightarrow -\infty \Longrightarrow e^x \rightarrow 0 \Longrightarrow e^{-\infty} \rightarrow 0
$$
- $arctanx$
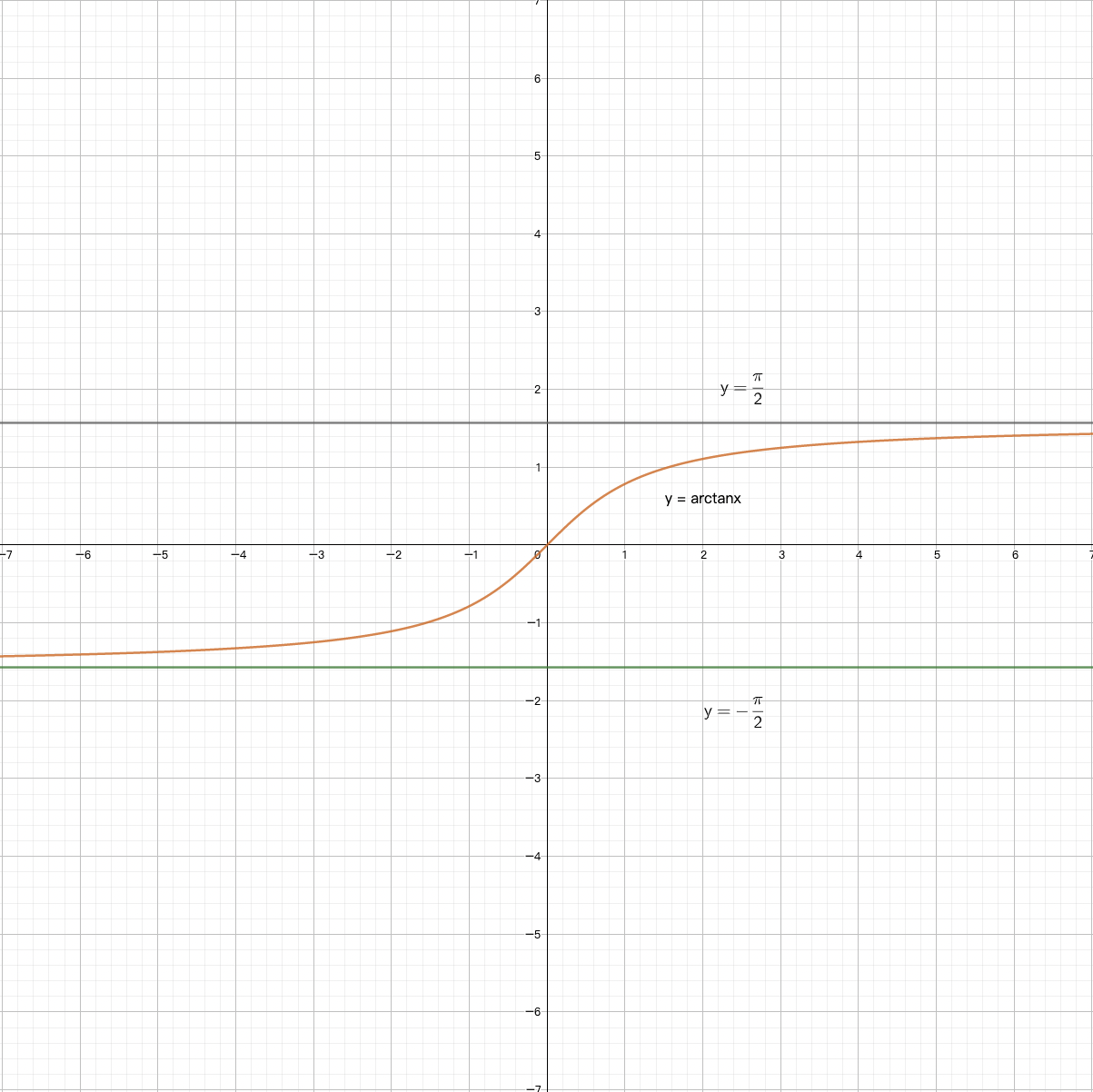$$
x \rightarrow \infty \
x \rightarrow +\infty \Longrightarrow arctanx \rightarrow \frac{\pi}{2} \
x \rightarrow -\infty \Longrightarrow arctanx \rightarrow -\frac{\pi}{2}
$$
常考虑左右极限的类型
- 分段函数分段点 -> 分段点
- 含绝对值的函数
$$ \mid x \mid = \begin{cases} x & x \gt 0 \ -x & x \leq 0 \ \end{cases} $$
- 遇 $e^\infty, \frac{C}{0}, arctan\infty, e^{\frac{1}{x}}$
$$ \lim\limits_{x\rightarrow x_0}e^{\frac{1}{x}} \ x \rightarrow 0^+ \rightarrow \frac{1}{x} \rightarrow \frac{1}{0^+} \rightarrow +\infty \Longrightarrow e^{\frac{1}{x}} \rightarrow e^{+\infty} \rightarrow +\infty \ x \rightarrow 0^- \rightarrow \frac{1}{x} \rightarrow \frac{1}{0^-} \rightarrow -\infty \Longrightarrow e^{\frac{1}{x}} \rightarrow e^{-\infty} \rightarrow 0 $$
间断
函数的连续
连续：在 $x_0$ 某领域， 有 左极限 = 右极限 = 函数值
极限值 = 函数值
函数的间断点及其类型
- 定义：函数在定义区间不再连续 => 间断
- 间断点：指函数不连续的点
- 间断点的分类
- 分类标准：以间断点的左右极限是否存在作为划分依据
第一类间断点：指函数左右极限均存在的间断
- 跳跃间断点：左极限 $\neq$ 右极限
- 可去间断点：左极限 $=$ 右极限
第二类间断点：左右极限不存在的间断点
-
无穷间断点：指左右极限为 $\infty$
-
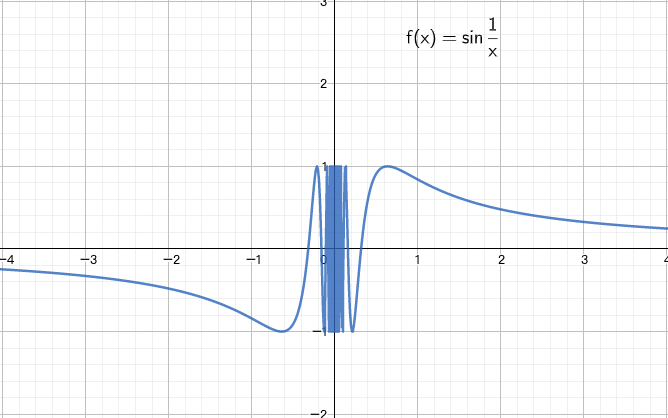
振荡间断点：指 $x \rightarrow x_0$ 时， 函数 $f(x)$ 剧烈波动，无定值
$x = 0$ 是 $f(x) = sin{\frac{1}{x}}$ 的振荡间断点
考点：间断点的判断
- 分式中， 分母 = 0 的点 => 必间断
- 分段函数的分段点 => 可能间断点
- 函数的无定义点 => 必间断
解题
- 找到可疑间断点
- 分别找到间断点的左右极限
- 根据左右极限情况定出间断点类型
无穷小量及其比较
无穷小量与无穷大量
- 无穷小量：若 $\lim\limits_{}f(x) = 0$ ，称此时的 $f(x)$ 为无穷小量。
- 无穷大量：若 $\lim\limits_{}f(x) = \infty$ ，称此时的 $f(x)$ 为无穷大量。
无穷小量与无穷大量的关系
$$ \frac{1}{无穷大量}=无穷小量 $$
$$ \frac{1}{不为0的无穷小量} = 无穷大量 $$
无穷小量加法运算：取次方最低。
无穷小量的比较
指比较无穷小量靠近0的速度快慢
无穷小量的阶：指 $x$ 的次方
设 $\alpha，\beta$ 是两个无穷小量
- 若 $\lim{}\frac{\beta}{\alpha} = C(常数) \neq 0$ ，则 $\alpha$ 与 $\beta$ 同阶
$$ \lim\limits_{x\rightarrow 0}\frac{2x^4}{3x^4} = \frac{2}{3} $$
- 若 $\lim{}\frac{\beta}{\alpha} = 1$ ，则 $\alpha$ $\sim$ $\beta$
- 若 $\lim{}\frac{\beta}{\alpha} = \infty$ ，则 $\alpha$ 比 $\beta$ 低阶
$$ \lim\limits_{x\rightarrow 0}\frac{2x^3}{4x^6} = \frac{1}{2}\lim\limits_{x\rightarrow 0}\frac{1}{x^3} = \infty $$
- 若 $\lim{}\frac{\beta}{\alpha} = 0$ ，则 $\alpha$ 比 $\beta$ 高阶
$$ \lim\limits_{x\rightarrow 0}\frac{4x^4}{x^3} = \lim\limits_{x\rightarrow 0}4x = 0 $$
- 若 $\lim{}\frac{\beta}{\alpha^{k}} = C(常数)$ ，则 $\beta$ 是 $\alpha$ 的 $k$ 阶无穷小
$$ x^3 是 x 的3阶 $$