概念及结论
绪论
数据:客观事务的符号表示,是所有能输入到计算机中并被计算机程序处理的符号总称
数据元素:数据的基本单位,在计算机中通常作为一个整体进行考虑和处理
数据项:组成数据元素的、有独立含义的,不可分割的最小单位
数据对象:性质相同的数据元素的集合,是数据的一个子集
数据类型:一个值的集合和定义在这个值集上的一组操作的总称
抽象数据类型: 一般指由用户定义的,表示应用问题的数学模型,以及定义在这个模型上的一组操作的总称,具体包括三部分:数据对象、数据对象上关系的集合以及对数据对象的基本操作的集合
逻辑结构:从逻辑关系上描述数据,它与数据的存储无关,是独立于计算机的
存储结构(又称物理结构):数据对象在计算机中的存储表示。把数据对象存储到计算机时,通常要求既要存储各数据元素的数据,又要存储数据元素之间的逻辑关系,数据元素在计算机内用一个结点表示。
算法的五个特性:==有穷性、确定性、可行性、输入、输出==
算法优劣的四个标准:==正确性、可读性、健壮性、高效性==
时间复杂度:重复语句被执行的次数
空间复杂度:算法所需存储空间的度量
线性表
线性表:由 $n$ ($n\ge0$)个数据特性相同的元素构成的有限序列
空表:线性表中元素的个数 $n$ ($n\ge0$)定义为线性表的长度,$n=0$ 时称为空表
单链表:采用链式存储结构的线性表,每个结点中只包含一个指针域
双向链表:采用链式存储结构的线性表,每个结点除一个数据域外,还有两个指针域,其一指向直接前驱,另一指向直接后继
循环链表:采用链式存储结构的线性表,表中最后一个结点的指针域指向头结点,整个链表形成一个环
单链表某结点p有后继结点的条件是:p.next != NULL
栈与队列
栈:限定仅在表尾进行插入或删除操作的线性表
队列:一种先进先出的线性表,它只允许在表的一端进行插入,而在另一端删除元素
循环队列:采用链式存储结构的队列并形成环状
front始终指向队首元素,rear指向队尾元素的下一个位置
- 队空条件:
front == rear - 队满条件:
(rear+1)%MaxSize == front - 入队:
rear = (rear+1) % (m+1) - 出队:
front = (front+1) % maxSize
循环队列的长度计算:
- rear=front:
0 - rear>front:
rear-front - rear<front:
(rear-front+maxSize) % maxSize
链队:
front始终指向队首元素,rear指向队尾元素的下一个位置
队空条件:front == rear
串、数组和广义表
串:是由零个或多个字符组成的有限序列
空串:零个字符的串
子串:串中的任意个连续的字符组成的子序列
主串:包含子串的串相应称为主串
串公式:
-
字串: n(n+1)/2 + 1
-
非空子串:n(n+1)/2
-
非空真子串:n(n+1)/2 - 1
数组:由类型相同的数据元素构成的有序集合
广义表:是由零个或多个单元素或子表所构成的有限序列,线性表的推广,也称为列表
树和二叉树
树:是 $n$ ($n\ge0$)个结点的有限集,它或为空树$(n=0)$; 或为非空树
二叉树:是 $n$ ($n\ge0$)个结点所构成的集合,它或为空树$(n=0)$; 或为非空树
满二叉树:深度为 $k$ 且有 $2^{k}-1$ 个结点的二叉树
完全二叉树:深度为 $k$ 的,有 $n$ 个结点的二叉树,当且仅当其每一个结点都与深度为 $k$ 的满二叉树中编号从 $1$ 至 $n$ 的结点一一对应时
遍历二叉树:是指按某条搜索路径巡访树中每个结点,使得每个结点均被访问一次,而且仅被访问一次
线索:指向结点前驱和后继的指针
线索二叉树:加上线索的二叉树
- 在一棵高度为 h 的完全二叉树中,所含结点个数不小于 ==$2^{h-1}$==
二叉树的性质
性质1:在二叉树的第 $i$ 层上至多有 $2^{i-1}$ 个结点。
性质2:深度为 $k$ 的二叉树至多有有 $2^{i}-1$ 个结点($k \ge 1$)
性质3:对任何一棵二叉树 $T$,如果其终端结点数为 $n_0$ ,度为 $2$ 的结点数为 $n_2$ ,则 $n_0 = n_2 + 1$
性质4:具有 $n$ 个结点的完全二叉树的深度为 $\lfloor log_{2}{n} \rfloor+1$ 。
性质5:如果对一棵有 $n$ 个结点的完全二叉树(其深度为 $\lfloor log_{2}{n} \rfloor+1$ )的结点按层序编号(从第一层到 $\lfloor log_{2}{n} \rfloor+1$ 层,每层从左到右),则对任一结点 $i(1\le{i}\le{n})$ ,有
- 如果 $i = 1$ ,则结点 $i$ 是二叉树的根,无双亲;如果 $i \gt 1$ ,则其双亲
PARENT(i)是结点 $\lfloor i/2 \rfloor$ - 如果 $2i \gt n$ ,则结点 $i$ 无左孩子(结点 $i$ 为叶子结点);否则其左孩子
LCHILD(i)的结点为 $2i$ - 如果 $2i+1 \gt n$ ,则结点 $i$ 无右孩子;否则其右孩子
RCHILD(i)的结点为 $2i+1$
二叉树的存储结构
顺序存储,链式存储
二叉树的遍历
先续遍历:根左右
中续遍历:左根右
后续遍历:左右根
层次遍历:从上往下 依层遍历
二叉排序树
二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree)或者二叉判定树(Binary decision tree)口诀:==左小右大==
树的存储结构
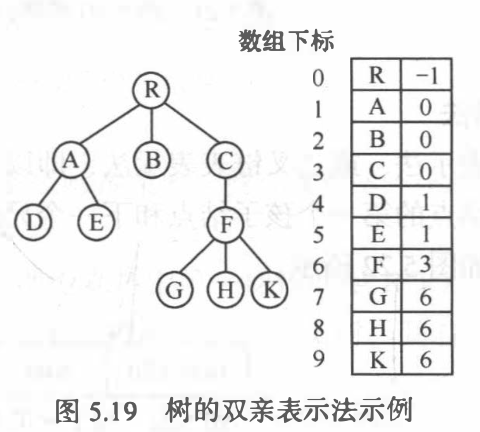
双亲表示法
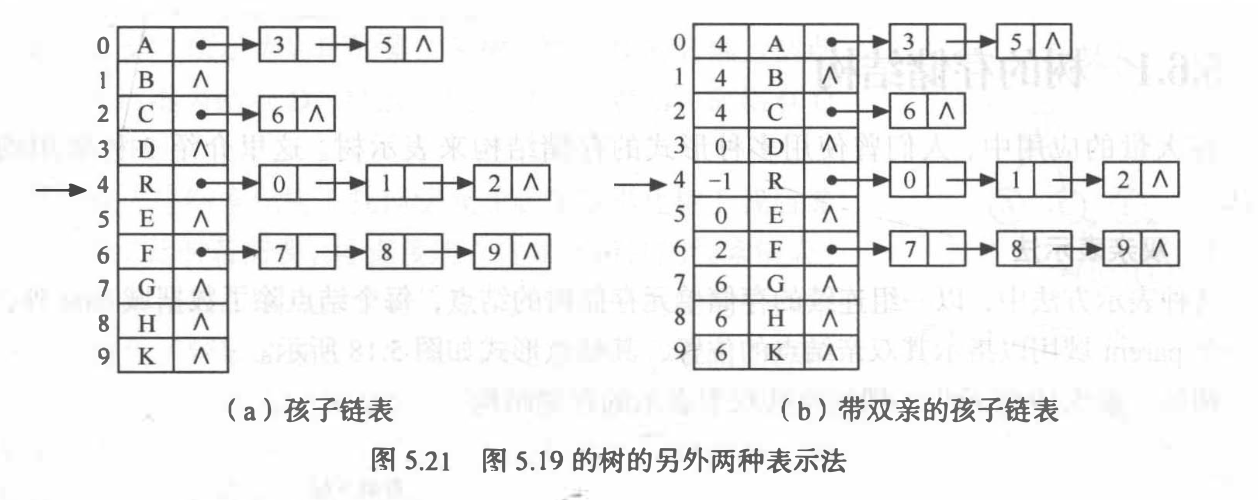
孩子表示法
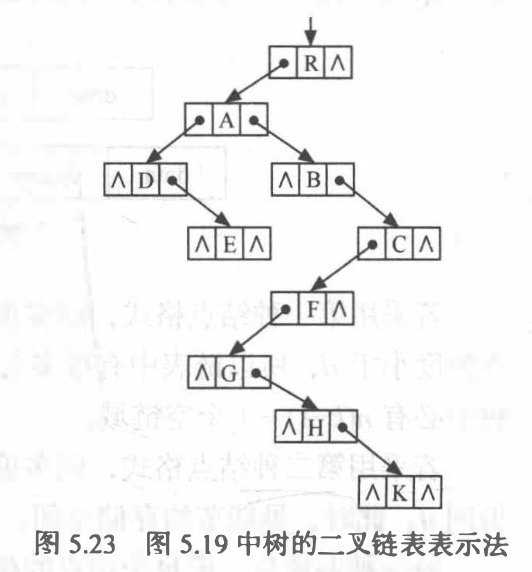
孩子兄弟表示法(二叉树表示法)
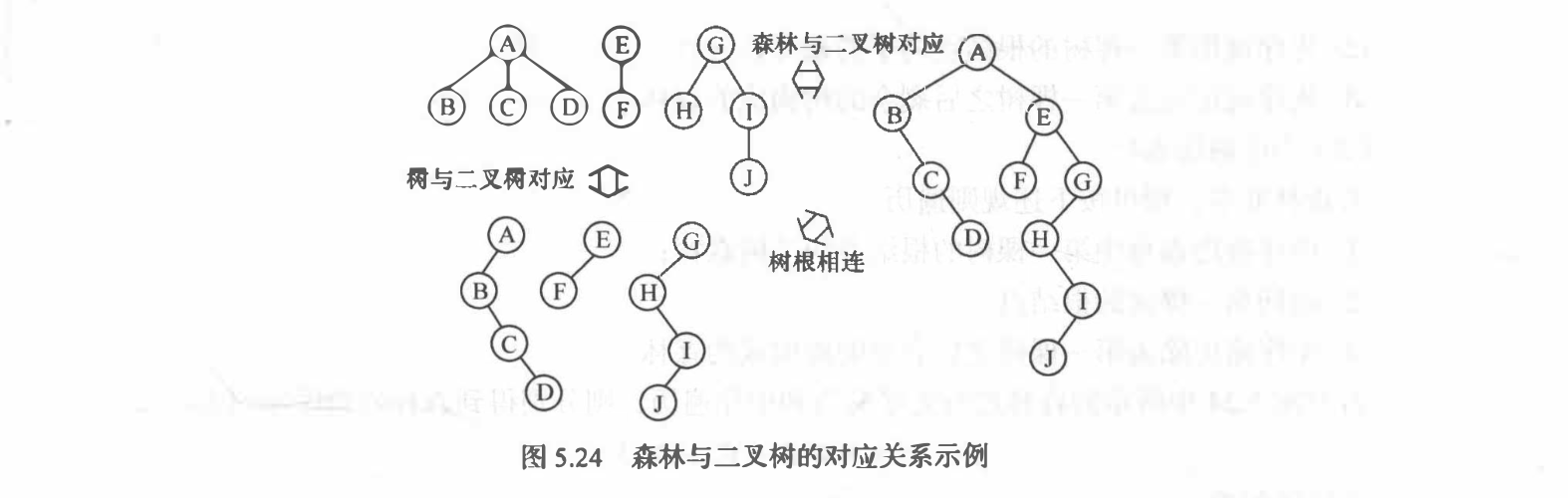
森林与二叉树的转换
森林转二叉树:==拼接右子树==
二叉树转森林:==去掉右子树==
树和森林的遍历
先根遍历:与二叉树的==先序遍历==顺序相同。
后根遍历:与二叉树的==中序遍历==顺序相同。
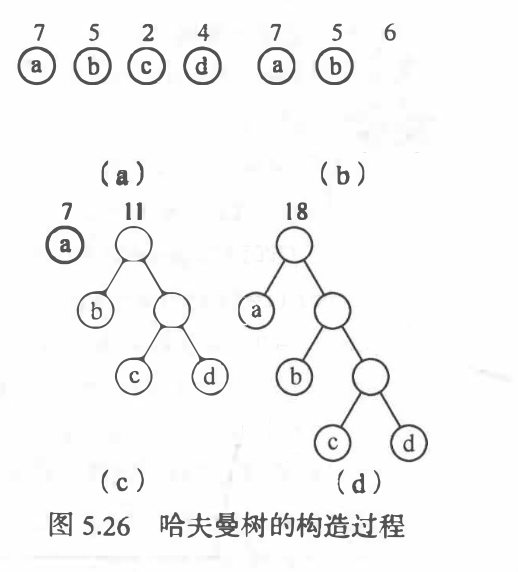
哈夫曼树
构建:
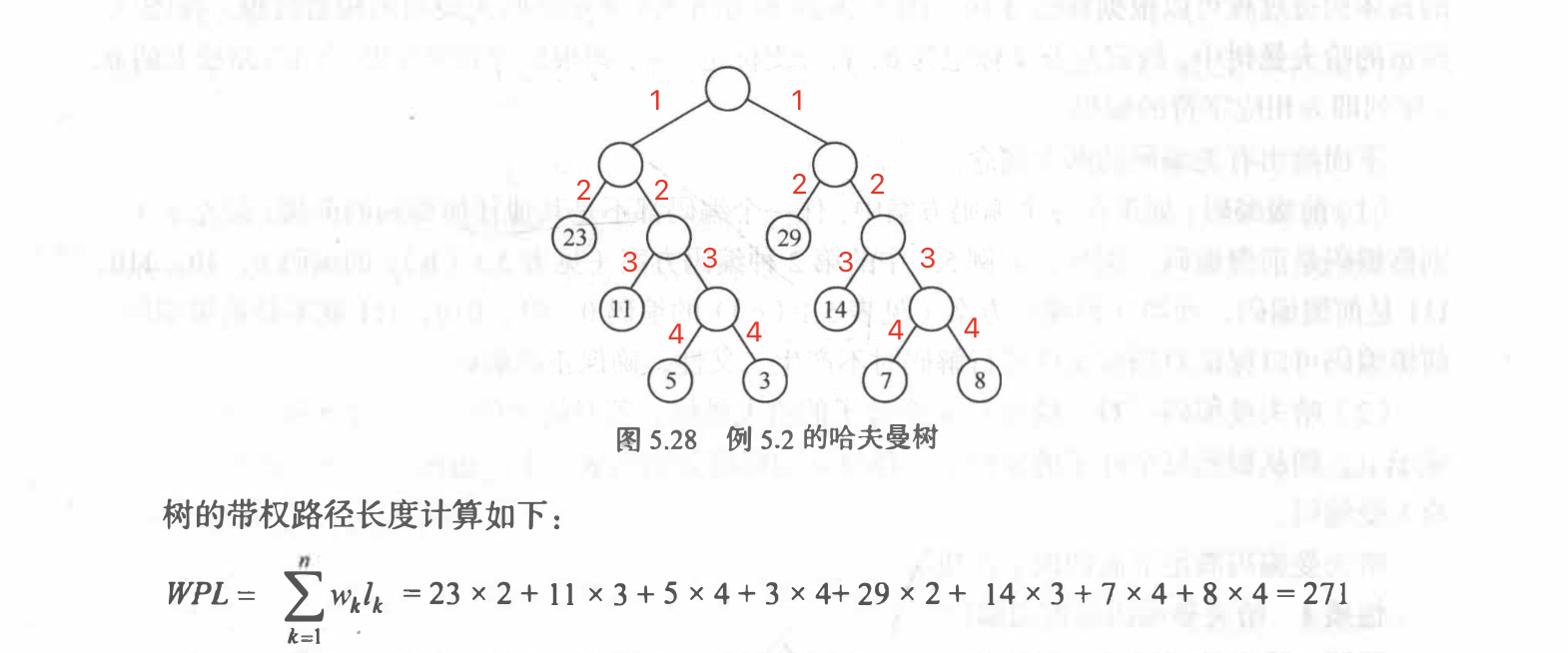
WPL(带权路径长度)最小的二叉树称为哈夫曼树,也称为最优二叉树
哈夫曼编码:==左 0 右 1==
图
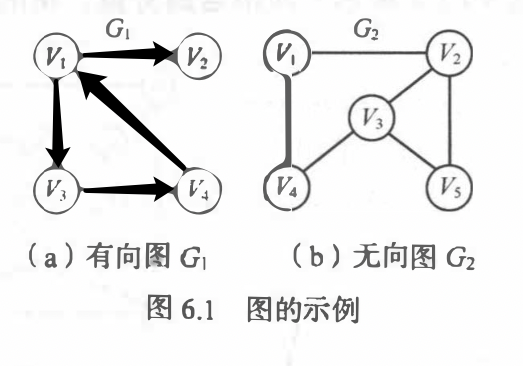
图:G由两个集合 V 和 E 组成, 记作 G=(V, E),其中V是顶点的有穷非空集合,E是V中的顶点偶对的有穷集合,这些顶点偶对称为边
有向图:有向边的集合
无向图:无向边的集合
无向完全图:具有 ==$n(n-1)/2$== 条边,最少有 ==$n-1$== 条边,
有向完全图:若具有 ==$n(n-1)$== 条弧
图的存储结构
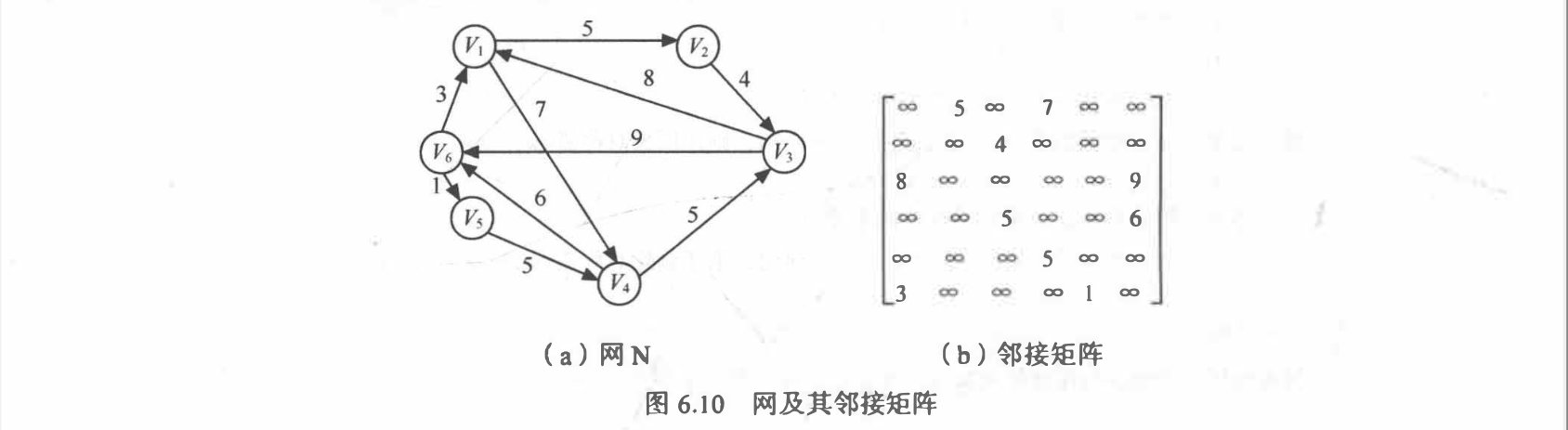
邻接矩阵表示法:表示顶点之间相邻关系的矩阵
$\infty$ 表示计算机允许的、 大于所有边上权值的数。例如, 图 6.10 所示 为一个有向网和它的邻接矩阵。
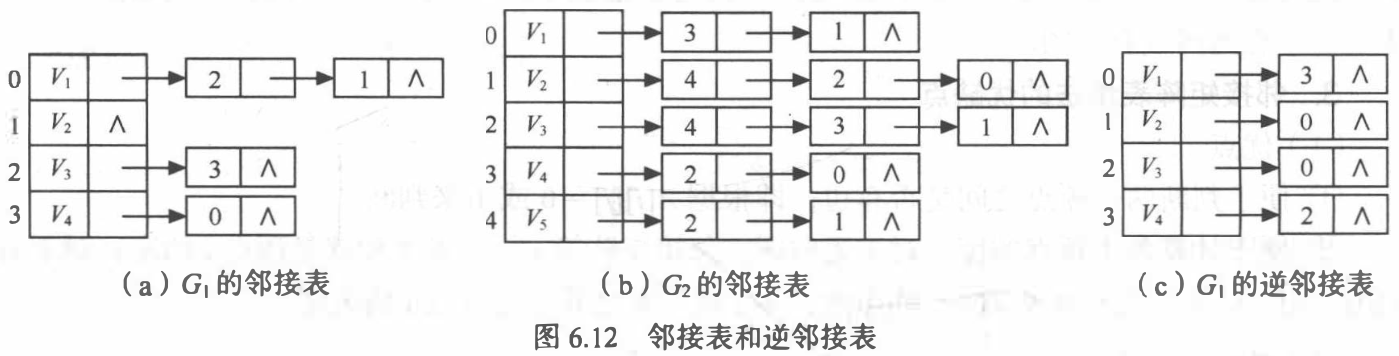
邻接表表示法:图的一种链式存储结构。邻接表由两部分组成:表头结点表和边表。
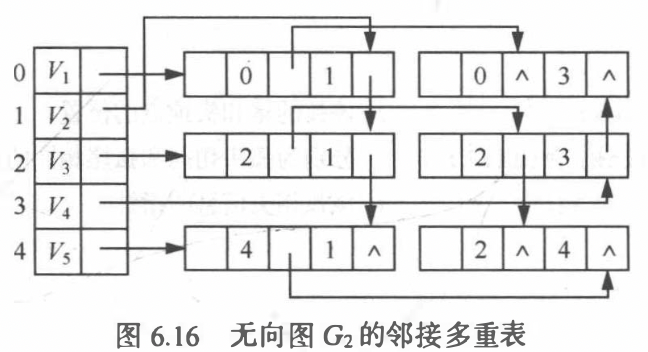
邻接多重表: 无向图的另一种链式存储结构
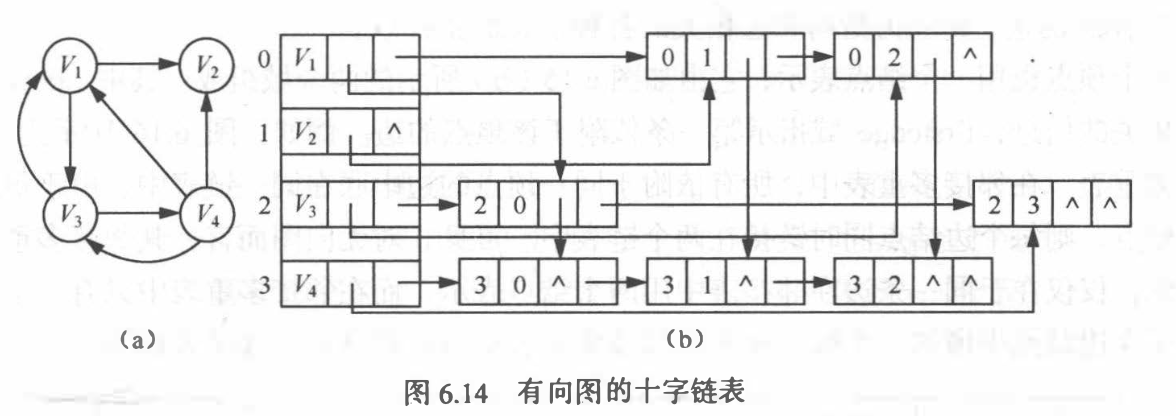
十字链表: 有向图的另一种链式存储结构
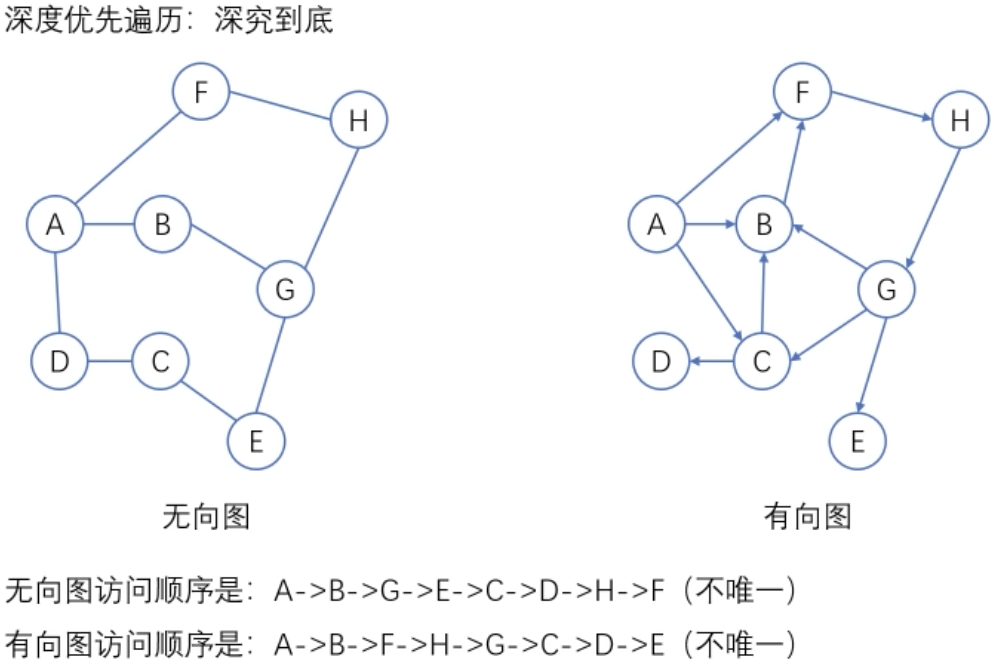
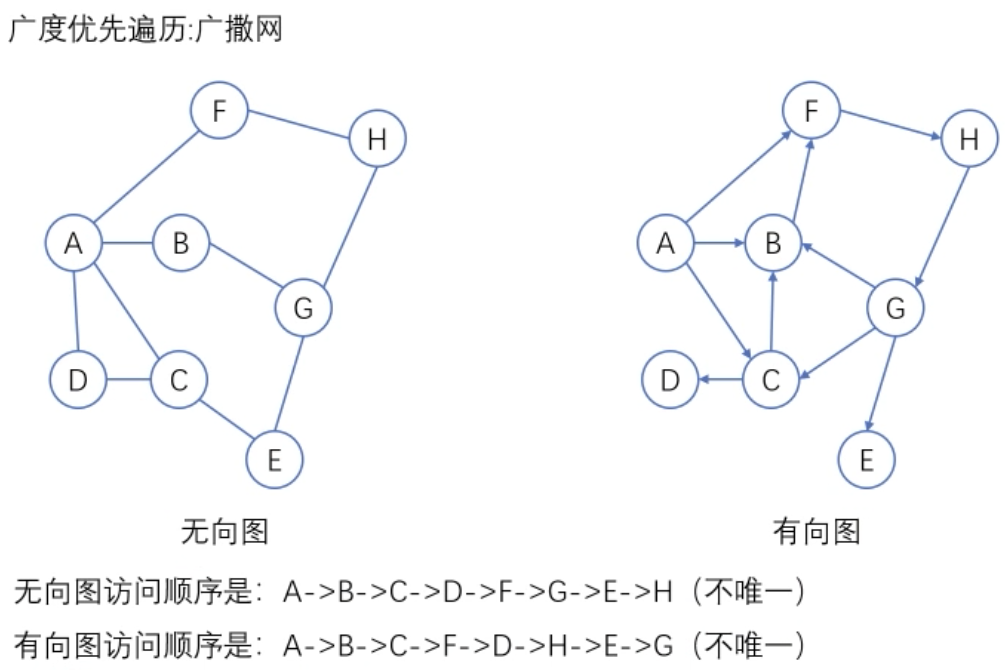
图的遍历
广度优先搜索:遍历类似于树的按层次遍历的过程
图的应用
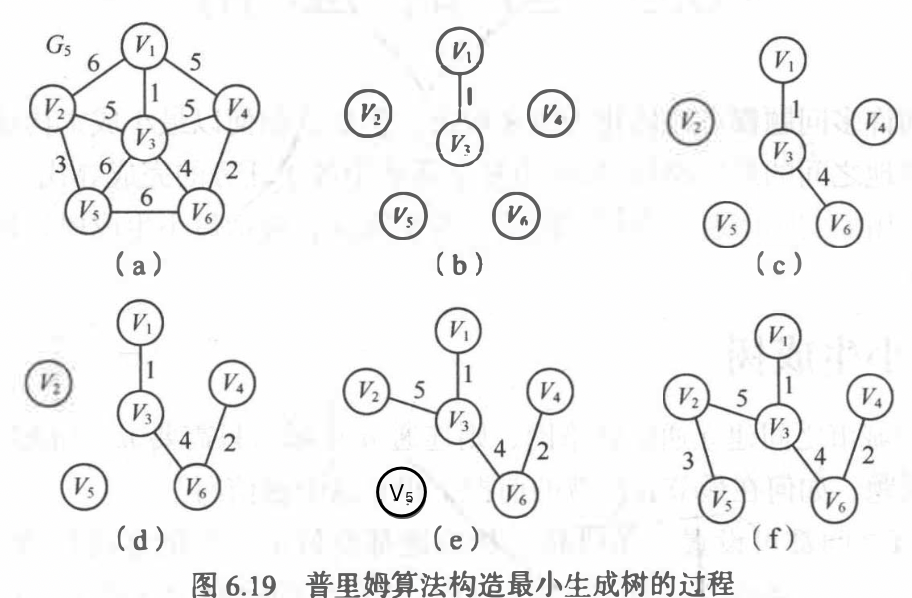
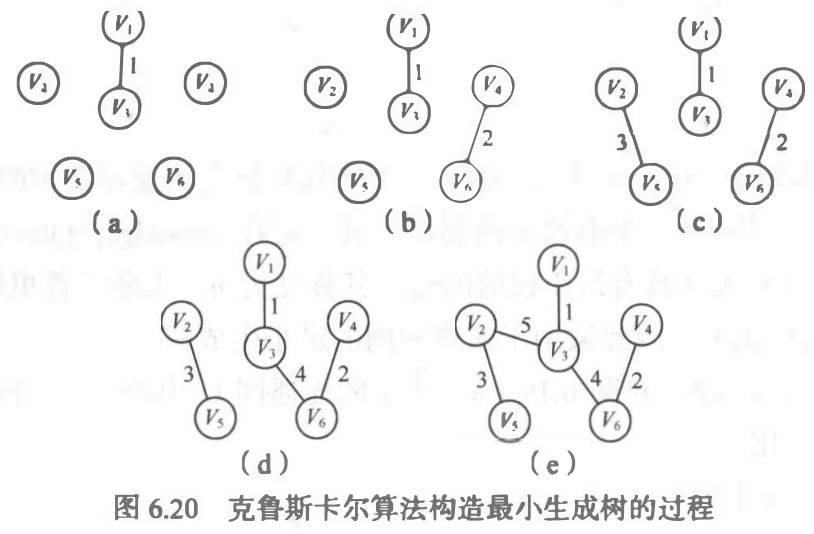
最小生成树
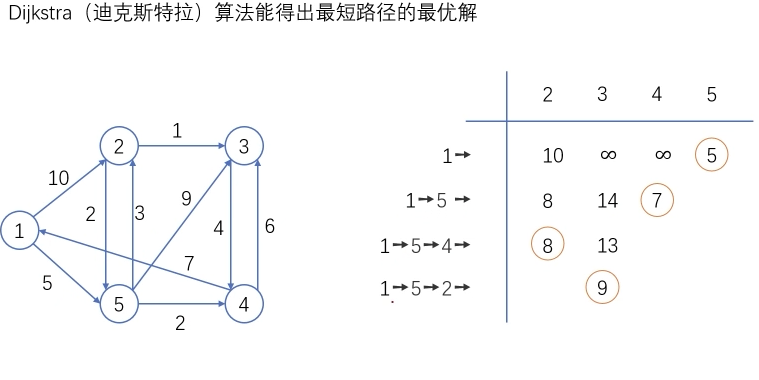
最短路径
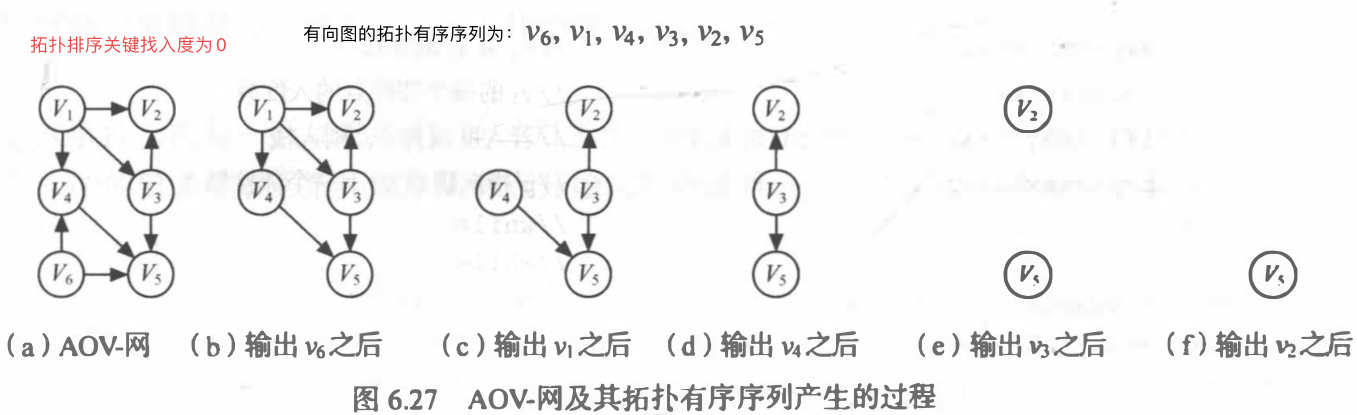
拓扑排序
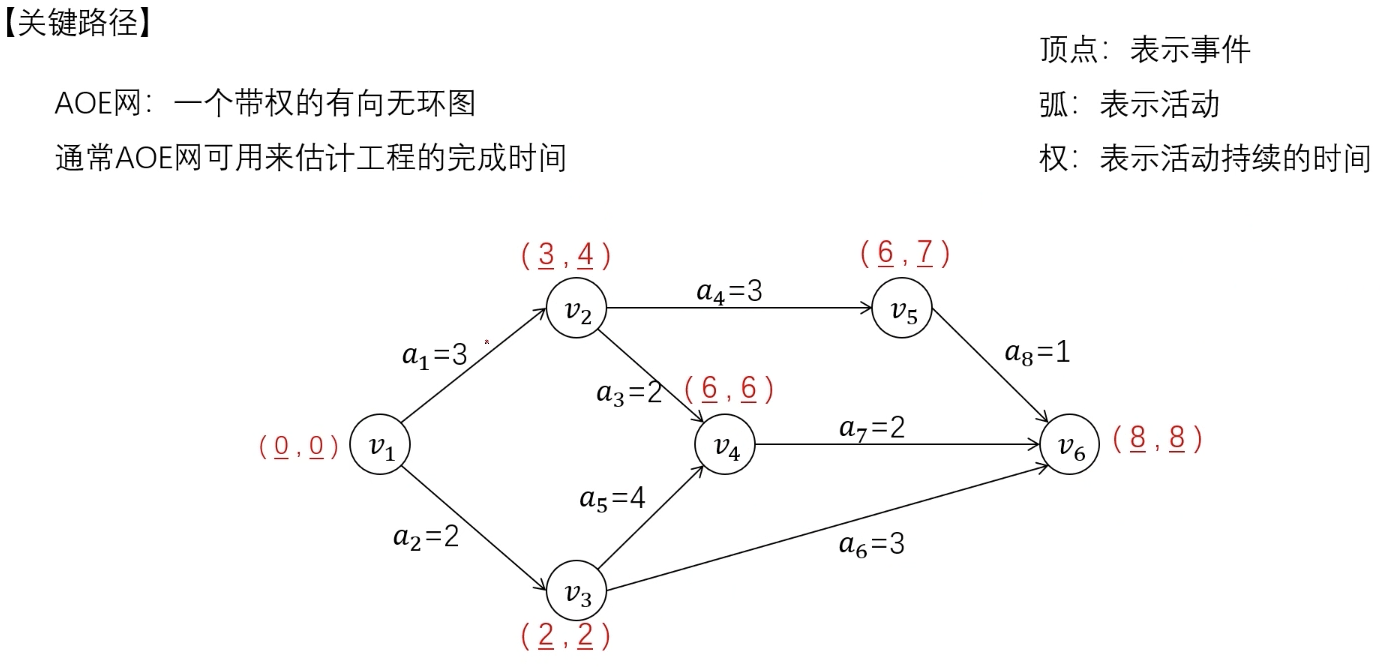
关键路径
关键路径:$v_1 \rightarrow v_3 \rightarrow v_4 \rightarrow v_6$
关键活动:$a_2, a_5, a_7$
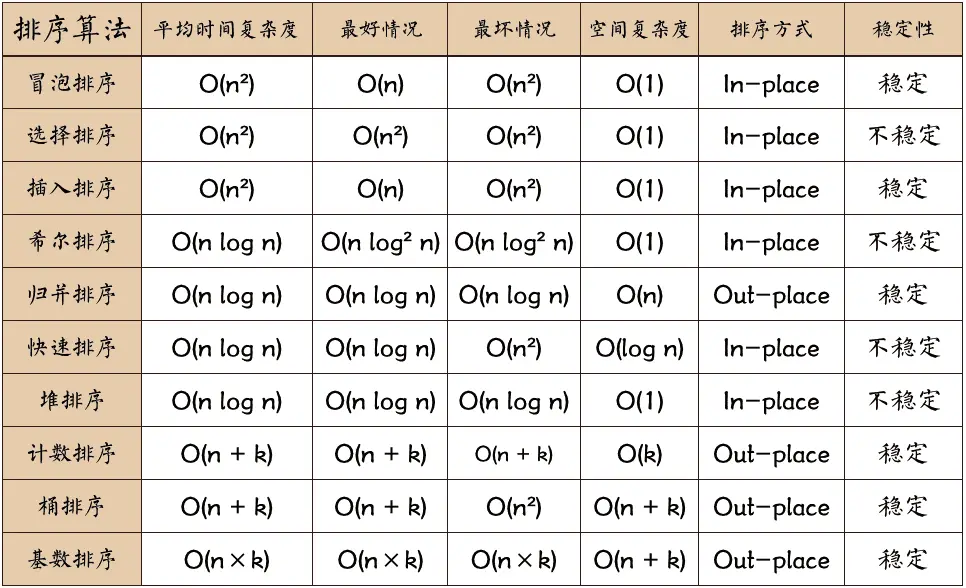
排序
散列表
散列表:一个有限连续的地址空间,用以存储按散列函数计算得到对应散列地址的数据记录
散列函数的构造方法:数学分析法、平方取中法、折叠法
散列函数处理冲突的方法:
-
开放地址法:
- 线性探测法
- 二次探测法
- 伪随机探测法
-
链地址法
ASL: 查找算法的查找成功时的平均查找长度
$ASL_{成功}$ = 散列表中已有元素查找成功的比较次数之和 / 散列表中的元素个数
$ASL_{失败}$ = 散列表中查找失败比较次数之和 / 散列表的散列函数的表长