第五章 树与二叉树
树的定义
树(Tree)是 $n$ ( $n\ge0$ )个结点的有限集,它或为空树($n=0$);或为非空树,对于非空书树 $T$ :
- 有且仅有一个称为根的结点;
- 除根结点以外的其余结点可分为 $m$ ( $m\gt0$ )个互不相交的有限集 $T_1,T_2,…,T_m$ ,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
树的基本术语
-
结点:树中的一个独立单元。
-
结点的度:结点拥有的子树数。
-
树的度:树内各结点度的最大值。
-
叶子(终端结点):度为 $0$ 的结点。
-
非终端结点(分支结点):度不为 $0$ 的结点。
-
双亲和孩子:结点的子树的根称为该结点的孩子,相应的,该结点称为孩子的双亲。
-
兄弟:同一个双亲的孩子之间互称兄弟。
-
祖先:从根到该结点所经分支上的所有结点。
-
子孙:以某结点为根的子树中的任意结点都称为该结点的子孙。
-
层次:结点的层次从根开始定义起,根为第一层,根的孩子为第二层。树的任意结点的层次等于其双亲结点的层次加1。
-
堂兄弟:双亲在同一层的结点互为堂兄弟。
-
树的深度(高度):树中结点的最大层次。
-
有序树和无序树:如果将树中结点的各子树看成从左至右是有次序的(即不能互换),则称该树为有序树,否则称为无序树。
-
森林:是 $m$ ( $m\ge0$ )棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林
二叉树
二叉树 (Binary Tree)是 $n$ ( $n\ge0$ )个结点所构成的集合,它或为空树($n=0$);或为非空树,对于非空树 $T$ :
- 有且仅有一个称为根的结点;
- 除根结点以外的其余结点分为两个互不相交的子集 $T_1$ 和 $T_2$ ,分别称为 $T$ 的左子树和右子树,且 $T_1$ 和 $T_2$ 本身又都是二叉树。
二叉树与树的区别
- 二叉树每个结点至多只有两棵子树(即二叉树不存在度大于2的结点);
- 二叉树的子树有左右之分,其次序不能任意颠倒。
二叉树的性质
- 在二叉树的第 $i$ 层上至多有 $2^{i-1}$ 个结点( $i\ge1$ )。
- 深度为 $k$ 的二叉树至多有 $2^{k}-1$ 个结点 ( $k\ge1$ )。
- 对任何一棵二叉树 $T$ ,如果其终端结点为 $n_0$ ,度为 $2$ 的结点数为 $n_2$ ,则 $n_0=n_{2}+1$ 。
满二叉树
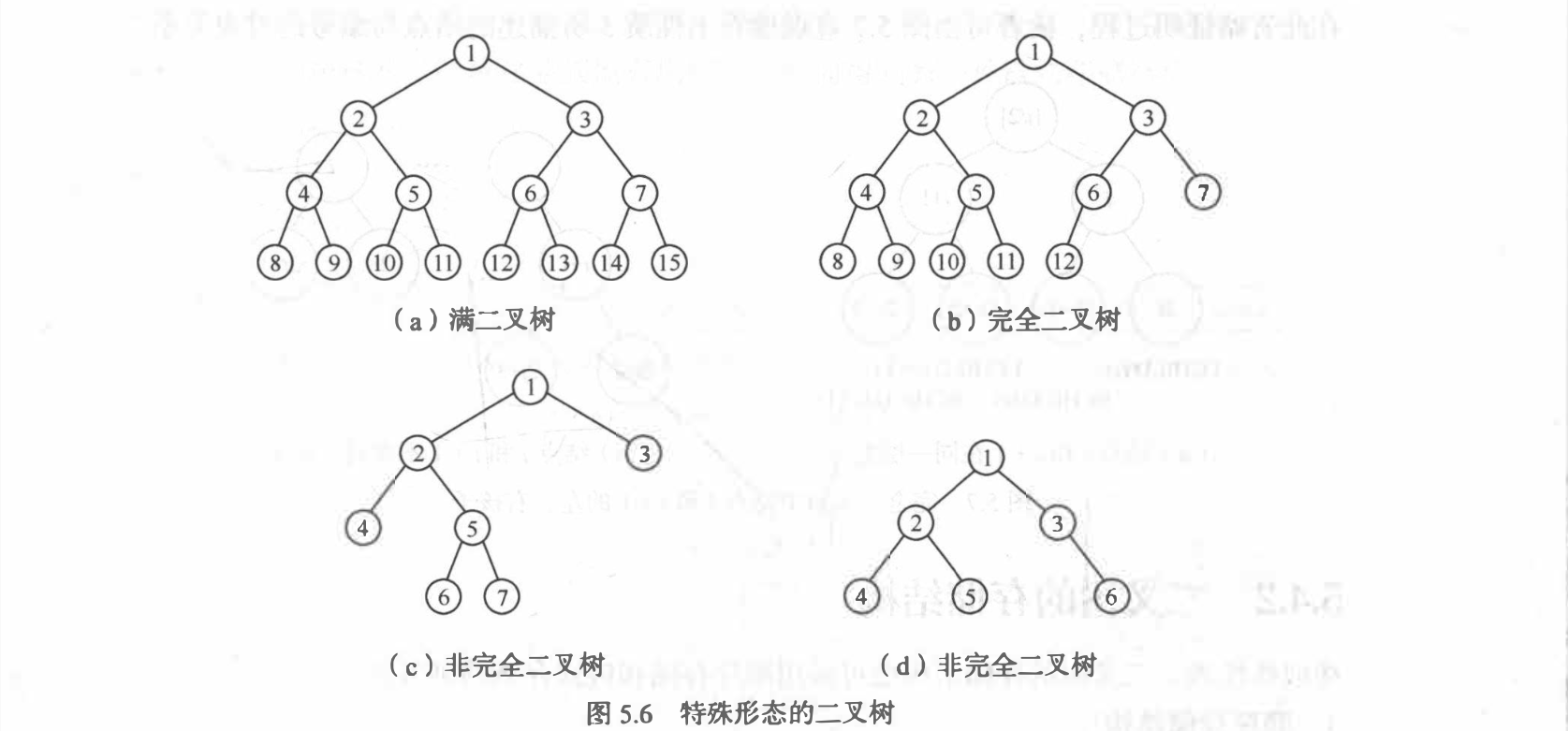
深度为 $k$ 且含有 $2^{k}-1$ 个结点的二叉树。图 5.6(a)所示是一棵深度为 $4$ 的满二叉树
特点:每一层上的结点数都是最大结点数,即每一层 $i$ 的结点数都具有最大值 $2^{i-1}$ 。
完全二叉树
深度为 $k$ 的,有 $n$ 个结点的二叉树,当且仅当其每一个结点都与深度为 $k$ 的满二叉树编号从 $1$ 至 $n$ 的结点一一对应时,称之为完全二叉树。图 5.6(b)所示为一棵深度为 $4$ 的完全二叉树
特点
- 叶子结点只可能在层次最大的两层上出现
- 对任一结点,若其右分支下的子孙的最大层次为 $l$ ,则其左分支下的字段的最大层次必为 $l$ 或 $l+1$ 。图 5.6(c)和(d)不是完全二叉树
性质
- 具有 $n$ 个结点的完全二叉树的深度为 $\lfloor log_{2}{n} \rfloor+1$ 。